1. Update the network status according to the predicted value (for single sequence data)
Dataset, source address: (you can use it directly)
It is placed in the comment area, but it cannot pass the review if it is placed in the text.
What is achieved is: given the data of the previous few years, the data of 100 days in 2023 is predicted in the future.
Step1: Load data and perform data preprocessing
clc
clear
load dataset.mat %加载数据(double型,剔除了2023年的的第一个数据,总共为2191个。时序预测没有实际时间,只有事情发生的顺序)
data=data(:,2)’; %不转置的话,无法训练lstm网络,显示维度不对。
%% 序列的前2000个用于训练,后191个用于验证神经网络,然后往后预测200个数据。
dataTrain = data(1:2000); %定义训练集
dataTest = data(2001:2191); %该数据是用来在最后与预测值进行对比的
%% 数据预处理
mu = mean(dataTrain); %求均值
sig = std(dataTrain); %求均差
dataTrainStandardized = (dataTrain – mu) / sig;
LSTM has high requirements for data standardization. And the reason why only the training set is standardized here is that the values in the neural network are only the training set, so there is no need to standardize the test set.
Step2: Alternate a time step
%% 输入的每个时间步,LSTM网络学习预测下一个时间步,这里交错一个时间步效果最好。
XTrain = dataTrainStandardized(1:end-1);
YTrain = dataTrainStandardized(2:end);
Most LSTM-related materials still use the default a=1 to split the time series into samples with input and output components. I used different a to observe in my other experiments (a=1,2,5,10). This a means that it specifies how many steps forward to predict at one time. The purpose of setting different prediction steps a is to observe whether the performance of the prediction model can be improved. However, some validations show that adding lag does not improve the performance of predictive models. In fact, it is also easy to understand that the accuracy of a single prediction is definitely higher than the accuracy of a two-step prediction.
a=1 means input [[1],[2],[3],…,[10]] corresponds to output [[2],[3],[4],…[11]], When a is 2, [[1],[2],[3],…,[10]] corresponds to [[2,3],[3,4],[4,5],.. .,[10,11].
What is the role of the alternate time step here?
Converts sequence data to make it static. Specifically, using a=1 differencing to remove growth trends in the data.
Transform time series problems into supervised learning problems. Specifically, the data is grouped into input and output patterns, and the observations at the previous time step can be used as input to predict the observations at the current time step.
Step3: Define LSTM network architecture and train
%% 一维特征lstm网络训练
numFeatures = 1; %特征为一维
numResponses = 1; %输出也是一维
numHiddenUnits = 200; %创建LSTM回归网络,指定LSTM层的隐含单元个数200。可调
layers = [ …
sequenceInputLayer(numFeatures) %输入层
lstmLayer(numHiddenUnits) % lstm层,如果是构建多层的LSTM模型,可以修改。
fullyConnectedLayer(numResponses) %为全连接层,是输出的维数。
regressionLayer]; %其计算回归问题的半均方误差模块 。即说明这不是在进行分类问题。
%指定训练选项,求解器设置为adam, 1000轮训练。
%梯度阈值设置为 1。指定初始学习率 0.01,在 125 轮训练后通过乘以因子 0.2 来降低学习率。
options = trainingOptions(‘adam’, …
‘MaxEpochs’,1000, …
‘GradientThreshold’,1, …
‘InitialLearnRate’,0.01, …
‘LearnRateSchedule’,’piecewise’, …%每当经过一定数量的时期时,学习率就会乘以一个系数。
‘LearnRateDropPeriod’,400, … %乘法之间的纪元数由“ LearnRateDropPeriod”控制。可调
‘LearnRateDropFactor’,0.15, … %乘法因子由参“ LearnRateDropFactor”控制,可调
‘Verbose’,0, … %如果将其设置为true,则有关训练进度的信息将被打印到命令窗口中。默认值为true。
‘Plots’,’training-progress’); %构建曲线图 将’training-progress’替换为none
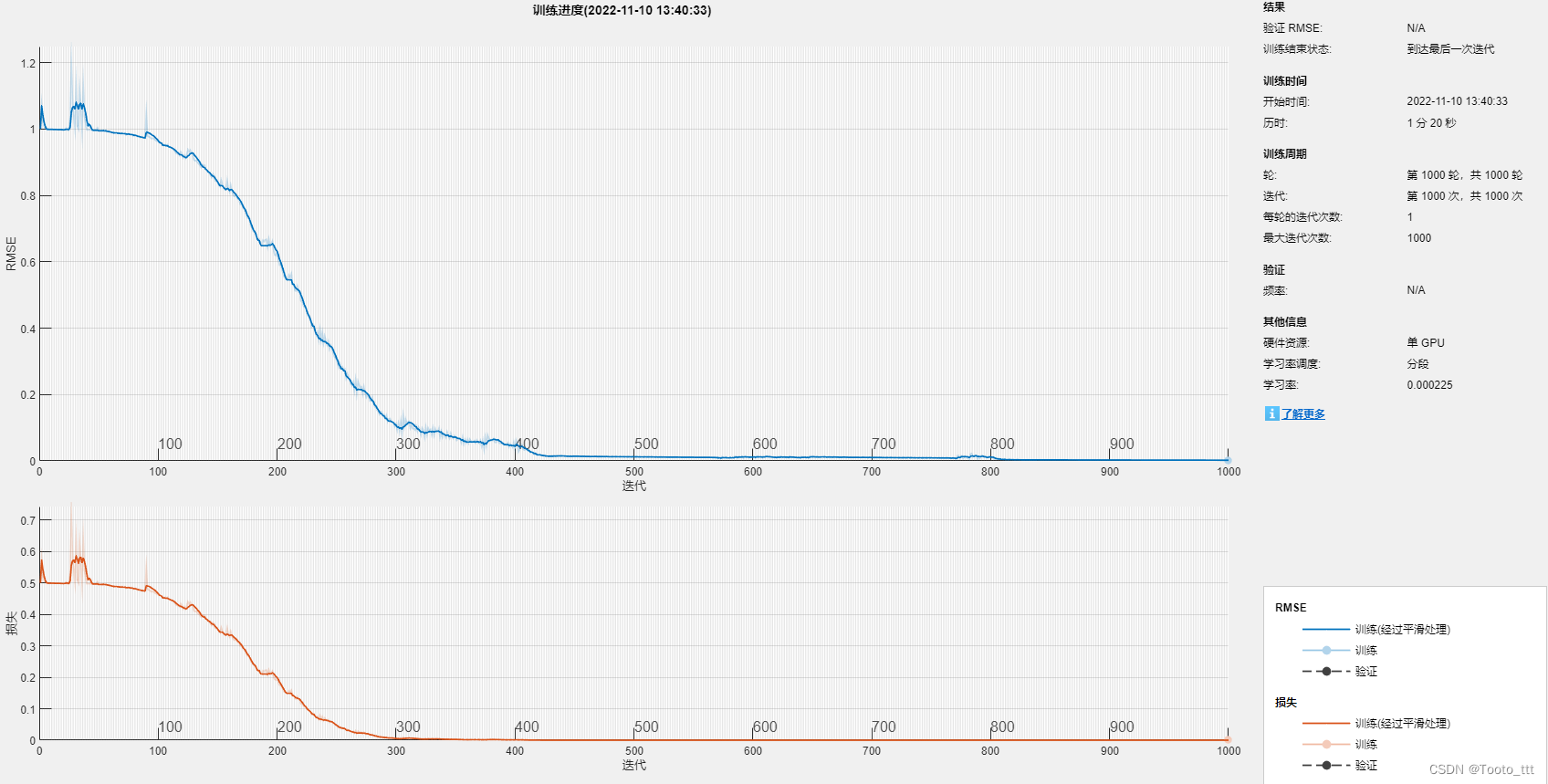
net = trainNetwork(XTrain,YTrain,layers,options);
It should be reminded that in MATLAB, the LSTM network has been packaged in the form of a toolbox, so the underlying “gate” concept is no longer involved. If you use Python to program, it will be involved.
There are three important parameters here. The first is numHiddenUnits, the second is LearnRateDropPeriod, and the third is LearnRateDropFactor. These three need to be changed according to your data set. If the RMSE curve drops too slowly, it may be due to the following reasons: (In this code, you need to increase the LearnRateDropPeriod.)

Step4: Initialize the network status
net = predictAndUpdateState(net,XTrain); %将新的XTrain数据用在网络上进行初始化网络状态
[net,YPred] = predictAndUpdateState(net,YTrain(end)); %用训练的最后一步来进行预测第一个预测值,给定一个初始值。这是用预测值更新网络状态特有的。
The last one for training, the first for prediction.
Step5: Use LSTM network for single-step prediction
%% 进行用于验证神经网络的数据预测(用预测值更新网络状态)
for i = 2:291 %从第二步开始,这里进行191次单步预测(191为用于验证的预测值,100为往后预测的值。一共291个)
[net,YPred(:,i)] = predictAndUpdateState(net,YPred(:,i-1),’ExecutionEnvironment’,’cpu’); %predictAndUpdateState函数是一次预测一个值并更新网络状态
end
In the NAR and NARx mentioned in other blogs, the recursive prediction will always accumulate errors, so that the performance will drop rapidly, but LSTM is unique to other networks in that it has this special function predictAndUpdateState that can update the network state every time it is predicted, so It is capable of predicting longer sequences.
Step6: Compare the predicted results with the actual data
%% 验证神经网络
YPred = sig*YPred + mu; %使用先前计算的参数对预测去标准化。
rmse = sqrt(mean((YPred(1:191)-dataTest).^2)) ; %计算均方根误差 (RMSE)。
subplot(2,1,1)
plot(dataTrain(1:end)) %先画出前面2000个数据,是训练数据。
hold on
idx = 2001:(2000+191); %为横坐标
plot(idx,YPred(1:191),’.-‘) %显示预测值
hold off
xlabel(“Time”)
ylabel(“Case”)
title(“Forecast”)
legend([“Observed” “Forecast”])
subplot(2,1,2)
plot(data)
xlabel(“Time”)
ylabel(“Case”)
title(“Dataset”)
%% 继续往后预测2023年的数据
figure(2)
idx = 2001:(2000+291); %为横坐标
plot(idx,YPred(1:291),’.-‘) %显示预测值
hold off
Step7: Reset the network status
net = resetState(net);
If other predictions are required, such as the next round of 300 predictions. The network status needs to be reset.
Training result:
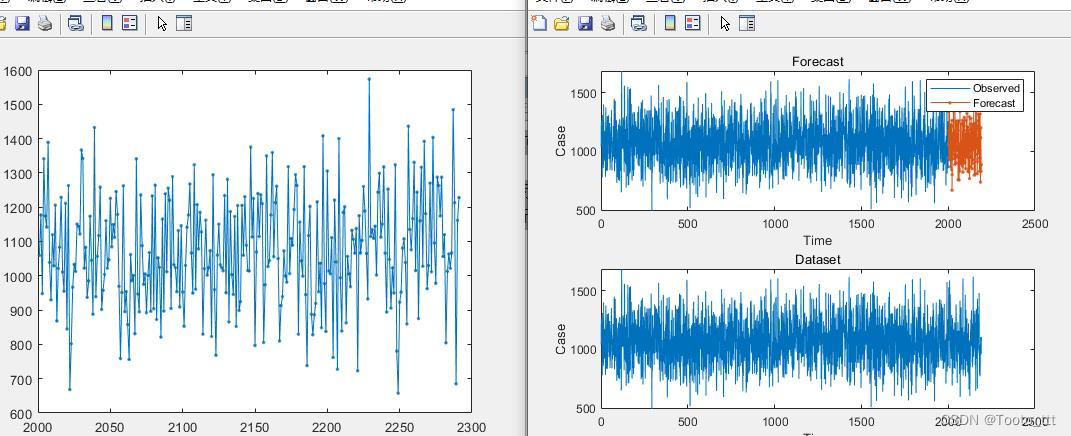
The picture on the left shows that starting from 2191, 100 predictions were made in the future. The picture on the right shows the use of 2001:2191 data to verify the training results of the neural network, which is relatively good here.
But when predicting, you can’t evaluate the quality of this data set solely from the number and ratio of the training set and the prediction set. In theory, the training set should contain changes in multiple cycles, otherwise it will definitely not be possible to make predictions through this. . And 100 data to predict 30 data does not mean that using 1000 data to predict the next 300 is the same performance, the two are different.
Ways to make the predictive model more accurate include increasing the dimensionality of the predictive input, i.e. adding different features (such as multiple coheometers mentioned below). At the same time, it should be noted that this model is only suitable for single-sequence prediction (that is, only the data of wave force is used to predict the subsequent wave force, so its prediction accuracy is actually not high.)
2. Update the network status according to the observation value (experimental, multi-sequence)
The requirement in the experiment is: use the wave height data of 5 wave height meters to predict the wave force after a certain interval (5 seconds). Therefore, what is needed for neural network training is a sufficient number of wave height and wave force data samples. In each step, the data of 5 wave height meters can be compared with the wave force data after 5 seconds. Since the experimental data cannot be disclosed, everyone can understand the code and use it according to their actual situation.
Step1: Load data and perform data preprocessing
%% 将所有测得的数据切分为7500个数据和对数据进行标准化,消除变量之间的量纲关系,使数据具有可比性。
load testdata.mat %其中第一列为时间,第二列至第六列为波高数据,第七列为波浪力数据。
dt=0.01 %这里的每一步的间隔为0.01秒,可根据实际实验采样频率情况来定。
time_lag=500; %这里指的是根据波高力数据预测5秒后的波浪力,这个间距可以自己根据实际来调整。
N_total=7500; %这里指的是7500个时间步
t=testdata(:,1); %时间,共有7500个。
std_scale=std(testdata(:,2:7)); %对波高数据和波浪力数据求标准差
testdata_norm(:,2:7) =normalize(testdata(:,2:7)); %将数据归一化
lag=500;
Step2: Construct a time series of alternating 5-second time intervals as the input and output of the neural network.
%% 首先先将时间步分割好
t_input=t(1:end-lag); %7000=7500-500。1:7000个
t_output=t(lag+1:end); %501:7500个
%% 分割波高数据和波浪力数据
height_input(1:5,:)=testdata_norm(1:end-lag,2:6)’; %因此这里height_input中的每一行是一个波高仪的数据,一共有5个波高仪,每个波高仪收集了1-7500个时间步的波高信息。然后这里波高作为输入,是只截取第1-7000个时间步的数据作为输入。
height_output(1,:)=testdata_norm(lag+1:end,7)’; %这里指的是第501~7500个时间步的波浪力作为输出。
%% 决定网络的输入、输出、总数
net_input=height_input; %1:7000,指代的是波高信息
net_output=height_output; %501:7500,指代的是波浪力信息
sample_size=length(height_output); %样本总数7000
Step3: Neural Network Training
%% 训练神经网络参数设定
numHiddenUnits =5; %指定LSTM层的隐含单元个数为5
train_ratio= 0.8; %划分用于神经网络训练的数据比例为总数的80%
LearnRateDropPeriod=50; %乘法之间的纪元数由“ LearnRateDropPeriod”控制
LearnRateDropFactor=0.5; %乘法因子由参“ LearnRateDropFactor”控制,
%% 定义训练时的时间步。
numTimeStepsTrain = floor(train_ratio*numel(net_input(1,:))); %一共为7000个*0.8=5600个
%% 交替一个时间步,可以交替多个时间步,但这里交替一个时间步的效果其实是最好的,详见那篇开头第二篇建立在python之上的文章。(真正想要改变往后预测时间的长短为lag这个变量。)
XTrain = net_input(:, 1: numTimeStepsTrain+1); %1~5601,XTrain—input,一共为5601个
YTrain = net_output(:, 2: numTimeStepsTrain+2); %2~5602,YTrain—expected output,为5601个
%% 输入有5个特征,输出有1个特征。
numFeatures = numel(net_input(:,1)); %5
numResponses = numel(net_output(:,1)); %1
layers = [ …
sequenceInputLayer(numFeatures) %输入层为5
lstmLayer(numHiddenUnits) %lstm层,构建5层的LSTM模型,
fullyConnectedLayer(numResponses) %为全连接层,是输出的维数。
regressionLayer]; %其计算回归问题的半均方误差模块 。即说明这不是在进行分类问题。
options = trainingOptions(‘adam’, … %指定训练选项,求解器设置为adam, 1000轮训练。
‘MaxEpochs’,150, … %最大训练周期为150
‘GradientThreshold’,1, … %梯度阈值设置为 1
‘InitialLearnRate’,0.01, … %指定初始学习率 0.01
‘LearnRateSchedule’,’piecewise’, … %每当经过一定数量的时期时,学习率就会乘以一个系数。
‘LearnRateDropPeriod’, LearnRateDropPeriod, …
‘LearnRateDropFactor’,LearnRateDropFactor, … %在50轮训练后通过乘以因子 0.5 来降低学习率。
‘Verbose’,0, … %如果将其设置为true,则有关训练进度的信息将被打印到命令窗口中,0即是不打印 。
‘Plots’,’training-progress’); %构建曲线图 ,不想构造就将’training-progress’替换为none
net = trainNetwork(XTrain,YTrain,layers,options); %训练神经网络
save(‘LSTM_net’, ‘net’); %将net保存为LSTM_net
end
Step4: Neural Network Prediction + Accuracy Reflection
%% 定义Xtest和Ytest,其目的是仿照神经网络训练中XTrain和YTrain的样式去构造一个测试集
%% input_Test指的是实验中得到的波高数据。
%% output_Test指的就是参与跟预测值进行对比的测量值。即expected output
numTimeStepsTrain2 = floor(0.1*sample_size); %一共为7000个*0.1=700个。可以自己再随意取一个比例,去尝试一下。当然也可以跟上面的numTimeStepsTrain保持一致。
input_Test = net_input(:, numTimeStepsTrain2+1: end-1); %7000个中取701个~6999,一共是6299个
output_Test = net_output(:, numTimeStepsTrain2+2: end); %7000个取702:7000,为6299个,因为 numTimeStepsTrain是700.
%% 这里首先用input_Train来初始化神经网络。经过测试,不是将整个input_Train放进去最好,放其中一点比例即可。
input_Train = net_input(:, floor(numTimeStepsTrain*0.9): numTimeStepsTrain); %630~700
net = predictAndUpdateState(net, input_Train);
%% 预测量预定义
rec_step=numel(output_Test); %滚动预测6299个。跟后面的j循环有关。
YPred=zeros(rec_step,1); %6299个预测,1个特征。这个预测是和Test来比对,看是否正确的。
%% 神经网络预测(这个也是之后实际预测需要用到的)
for j=1: rec_step
[net,YPred0] = predictAndUpdateState(net, input_Test(:, j)); %用input_Test代入刚刚用input_Train来更新的网络得到第一个输出并得到对应的预测值。
YPred(j, 🙂 = YPred0; %记录输出的预测值。
end
%% 神经网络精度反映。这里的Y都是波浪力
YTest = output_Test(:,1:rec_step)’; %这一步可以简化。其实只是一个转置。
NRMSE=sqrt(sum((YPred-YTest).^2)/rec_step/(max(YTest)-min(YTest)));
What needs to be emphasized here is the problem of using input_Train to initialize the neural network. Because in LSTM, the state cell is updated in real time, but it needs to be given an initialization value for the entire network, but it is not necessarily the best effect of using the entire input_Train, so in actual use, input_Train can consider giving a ratio to come Let it initialize.
Step5: Practical application of neural network
rec_step=2; %这里只预测两步
input_Test=[1;2;3;4;5,6;4;8;9;7]; %假设第一个时间步波高数据分别为1,2,3,4,5,第二个时间步波高数据分别为6;4;8;9;7。
%% 神经网络预测
for j=1: rec_step
[net,YPred0] = predictAndUpdateState(net, input_Test(:, j)); %用input_Test代入刚刚用input_Train来更新的网络得到第一个输出并得到对应的预测值。
YPred(j, 🙂 = YPred0; %记录输出2个的预测值。
end
Assuming that 5 wave height meter data have been obtained at the same time, it is necessary to predict the wave force after 5 seconds (preset in the previous neural network training). The wave height data obtained each time should be placed in the for loop to continuously perform single-step predictions.

On the left is the dataset, on the right is the prediction, my input in the prediction is the wave height 2 seconds ago, and the wave force after 2 seconds is predicted. This is equivalent to multiple single-step predictions, and it is quite accurate.



